Before we go any further, and especially before you start judging my code, I need to make a few disclaimers:
- I am not a python developer; so if you think my python sucks, then, well, you’re probably right,
- by no means am I an expert in evolutionary algorithms; the code that follows is just my attempt at making sense of a genetic algorithm through coding a simple implementation, driven by curiosity and overabundance of time to spare,
- performance was not my main focus; what I wanted to achieve is a rather easy-to-understand code that can be easily mapped into the concepts described in the literature.
I have decided to implement everything from scratch, mostly based on two books on the topic [1][2]. The term Simple Genetic Algorithm is used here in the same context as described by the author in [1]. With that in mind, if you spot any mistakes in the implementation, I will appreciate the feedback.
what is a genetic algorithm anyway?
A genetic algorithm is a way of finding a solution to a problem, inspired by biology, or evolution to be more precise (here’s a decent refresher on the topic if you need one). It is also the most popular variant from a broader class of evolutionary algorithms. The basic idea is to start with a set of random solutions (or good ones, in case you already have a decent knowledge of the domain and know what a good solution might look like). The solutions are then iteratively assessed and the best ones are selected from the pool, cross-bred, and mutated. This process repeated a fixed number of times (generations), or until a perfect solution is found, leads to (hopefully) better answers over time.
the problem to solve
We are going to apply those principles, one step at a time, to a simple, somewhat artificial, problem. You might think that using a genetic algorithm to solve it would be equivalent to killing a fly with a tank. And you wouldn’t be wrong. But, for the sake of this article, let’s pretend calculators haven’t been invented yet, and this is the best way to figure out the maximum square of an integer in the range 0–1048575 (inclusive).
bird’s-eye view
Before going into the details of implementation, let’s have a quick look at a high-level overview of the algorithm:
- Start with a bunch of solutions, likely random ones.
- Assess how good they are.
- Pick some that will be used to create new, ideally better, solutions.
- Create pairs from the selected bunch. Each pair will produce two new solutions.
- Make small random changes, with some probability, to the newly created solutions.
- Replace the previous bunch with the newly created solutions.
- Keep going till a perfect solution is found, you’re finally bored, or you have reached the heat death of the universe.
individuals, populations and fitness
Each solution, in the context of evolutionary algorithms, is called an individual. A set of individuals being considered as solutions at a given time is called a population.
Each individual can be characterised by its genotype. The genotype is the representation of the solution on which the algorithm operates directly. An actual solution in the domain of the problem is called the individual’s phenotype (a genotype always translates to a single phenotype however a specific phenotype might be obtained by multiple different genotypes).
To make this a bit more concrete, let’s consider what this would mean in the context of our problem. The genotype we are going to use to represent the individuals is going to be a binary number. The phenotype is going to be the square of that, expressed as a decimal integer.
To represent the range of integers we operate on, we are going to need a genotype of length 20 (2²⁰ = 1048576), which means genotypes between 00000000000000000000 (0 in binary) and 11111111111111111111 (1048575 in binary). For example, a phenotype of an individual with a genotype of 00000000000000000101 is going to be equal to 25 (5²).
Fitness is a measure of how good the solution is. In our case, we can simply use the individual’s phenotype as its fitness: the bigger the square of the number representing an individual’s genotype, the higher its fitness. In the example above, the fitness of the individual would be equal to 25.
Let’s have a look at some code:
class GenotypeDecoder:
def decode(self, genotype: str):
return int(genotype, 2) ** 2
class FitnessEvaluator:
def __init__(self, genotype_decoder: GenotypeDecoder):
self.genotype_decoder = genotype_decoder
def evaluate(self, genotype: str):
return self.genotype_decoder.decode(genotype)The GenotypeDecoder class is used to translate between a genotype, here represented as a binary number string, and a corresponding phenotype. FitnessEvaluator assesses the fitness of a given genotype. In our case, this directly corresponds to the individual’s phenotype, so the decoder is used.
class Individual:
def __init__(self, genotype: str, fitness: int):
self.genotype = genotype
self.fitness = fitness
def __repr__(self):
return "Individual/genotype = " + self.genotype + " Fitness = " + str(self.fitness)
class IndividualFactory:
def __init__(self, genotype_length: int, fitness_evaluator: FitnessEvaluator):
self.genotype_length = genotype_length
self.fitness_evaluator = fitness_evaluator
# E.g. {:032b} to format a number on 32 bits with leading zeros
self.binary_string_format = '{:0' + str(self.genotype_length) + 'b}'
def with_random_genotype(self):
genotype_max_value = 2 ** self.genotype_length
random_genotype = self.binary_string_format.format(random.randint(0, genotype_max_value))
fitness = self.fitness_evaluator.evaluate(random_genotype)
return Individual(random_genotype, fitness)
def with_set_genotype(self, genotype: str):
fitness = self.fitness_evaluator.evaluate(genotype)
return Individual(genotype, fitness)
def with_minimal_fitness(self):
minimal_fitness_genotype = self.binary_string_format.format(0)
fitness = self.fitness_evaluator.evaluate(minimal_fitness_genotype)
return Individual(minimal_fitness_genotype, fitness)An Individual has two properties: genotype and fitness. IndividualFactory wraps the new individual creation logic and provides three methods of doing so:
with_random_genotypecreates an individual with a random genotype- used at the very beginning to create a random population as a starting point,with_set_genotypecreates an individual with a provided genotype- used when a new individual is created through the breeding of two individuals from the previous generation,with_minimal_fitnesscreates an individual with a genotype consisting solely of zeros- used to create an alternative starting point with a population of individuals with fitness = 0.
class Population:
def __init__(self, individuals):
self.individuals = individuals
def get_the_fittest(self, n: int):
self.__sort_by_fitness()
return self.individuals[:n]
def __sort_by_fitness(self):
self.individuals.sort(key = self.__individual_fitness_sort_key, reverse = True)
def __individual_fitness_sort_key(self, individual: Individual):
return individual.fitness
class PopulationFactory:
def __init__(self, individual_factory: IndividualFactory):
self.individual_factory = individual_factory
def with_random_individuals(self, size: int):
individuals = []
for i in range(size):
individuals.append(self.individual_factory.with_random_genotype())
return Population(individuals)
def with_individuals(self, individuals):
return Population(individuals)
def with_minimal_fitness_individuals(self, size: int):
individuals = []
for i in range(size):
individuals.append(self.individual_factory.with_minimal_fitness())
return Population(individuals)Population class holds a collection of individuals. It provides a way of getting the fittest individuals through get_the_fittest method. PopulationFactory is a counterpart of IndividualFactory and provides methods of creating populations with random individuals, with given individuals, and with minimal-fitness individuals.
parent selection and survival selection
The first step to creating a new generation of solutions is selecting individuals from the current population that will become the parents (parent selection). The newly created individuals are called offspring. Deciding on which individuals to keep for the next generation is called survival selection.
There are many possible approaches to making the parent selection. In our example, we are going to go with a fitness proportional selection– the probability of an individual becoming a parent depends directly on their fitness. For this, we are going to use Stochastic Universal Sampling.
The basic idea here is to create a scale, composed of the fitness values of all the individuals in the population, which is then traversed in 1/pool size steps, starting at a random point p, such that 0 < p < 1/population size. For example, say our mating pool consists of individuals with fitness values 1, 5, 3, 12, 9, 6. To visualise the scale, imagine a ruler with following values marked on it:
[0, 1, 6, 9, 21, 30, 36]We start at 0 and we add a new fitness value to the previous mark on the ruler, so 0 -> 0 + 1 = 1 -> 1 + 5 = 6 -> 6 + 3 = 9 -> etc.
Now we pick a step at which we will travel along the ruler. The total fitness is equal to 36 (1 + 5 + 3 + 12 + 9 + 6), and there are 6 individuals in the population, so we are going to pick a random number from the range (0, 36/6 = 6) as the initial offset. The step size would be equal to 36/6 = 6.
Let’s assume our random offset is 2. We start at 2 and check on our ruler which individual this corresponds to- in this case the individual with index 1 (range between 1 and 6 on the ruler)- so this individual will be picked to a mating pool. We add the step to the current position, so 2 + 6 = 8. We repeat the same procedure as before, adding the second individual to the pool (range between 6 and 9). We keep repeating this process until we have reached the end of the ruler and end up with a collection of 6 individuals that will produce the next generation.
class ParentSelector:
def select_parents(self, population: Population):
total_fitness = 0
fitness_scale = []
for index, individual in enumerate(population.individuals):
total_fitness += individual.fitness
if index == 0:
fitness_scale.append(individual.fitness)
else:
fitness_scale.append(individual.fitness + fitness_scale[index - 1])
# Store the selected parents
mating_pool = []
# Equal to the size of the population
number_of_parents = len(population.individuals)
# How fast we move along the fitness scale
fitness_step = total_fitness / number_of_parents
random_offset = random.uniform(0, fitness_step)
# Iterate over the parents size range and for each:
# - generate pointer position on the fitnss scale
# - pick the parent who corresponds to the current pointer position and add them to the mating pool
current_fitess_pointer = random_offset
last_fitness_scale_position = 0
for index in range(len(population.individuals)):
for fitness_scale_position in range(last_fitness_scale_position, len(fitness_scale)):
if fitness_scale[fitness_scale_position] >= current_fitess_pointer:
mating_pool.append(population.individuals[fitness_scale_position])
last_fitness_scale_position = fitness_scale_position
break
current_fitess_pointer += fitness_step
return mating_poolThe selected individuals constitute a mating pool. In our example, its size is equal to the size of the population. This does not mean however that we select every individual. Some individuals with low fitness won’t make it to the pool at all. The highly fit ones, on the other hand, will be present in the pool more than once. This way the best solutions are more likely to produce offspring, and therefore have, on average, a bigger impact on the next generation.
In our implementation, each new generation will completely replace the previous generation. This, combined with the fact that each pair of parents will produce two children, will lead to constant population size.
breeding and mutation
Only selecting the fittest parents would not take us very far on its own. We need a way of transferring the features that make an individual fit to the next generation. This is where crossover, or in our case one-point crossover to be more precise, comes in.
Crossover is yet another term taken straight from biology and means combining the genotypes of two individuals (parents) into a new pair. For example, if the parents have genotypes of 00000111110000011111 and 11111111110000000000, first we select a random crossover point greater than 0 and smaller than the length of a genotype (in this case 20), say 7. This means we split both genotypes at the 7th (0 indexed) position:
1a) 0000011 1b) 1110000011111
2a) 1111111 2b) 1110000000000Now we create a new pair of genotypes by combining the first part of the first genotype (1a) with the second part of the second (2b) and the first part of the second genotype (2a) with the second part of the first genotype (1b):
1a) 0000011 2b) 1110000000000
2a) 1111111 1b) 1110000011111The new genotypes will become the offspring.
class SinglePointCrossover:
def __init__(self, individual_factory: IndividualFactory):
self.individual_factory = individual_factory
def crossover(self, parent_1: Individual, parent_2: Individual):
crossover_point = random.randint(0, len(parent_1.genotype))
genotype_1 = self.__new_genotype(crossover_point, parent_1, parent_2)
genotype_2 = self.__new_genotype(crossover_point, parent_2, parent_1)
child_1 = self.individual_factory.with_set_genotype(genotype = genotype_1)
child_2 = self.individual_factory.with_set_genotype(genotype = genotype_2)
return child_1, child_2
def __new_genotype(self, crossover_point: int, parent_1: Individual, parent_2: Individual):
return parent_1.genotype[:crossover_point] + parent_2.genotype[crossover_point:]In addition to using the existing solutions as a base for the new individuals, we also want to introduce some randomness to the process (as is the case in biological reproduction). This is achieved by employing mutation. Each bit (gene) in the genotype created with crossover has a small probability of being flipped (0 turning into 1 and vice versa) as the final stage of creating a new individual. In our example, we are going to use a probability of 1/genotype length for each gene mutating, so in this case 1/20 = 0.05.
class Mutator:
def __init__(self, individual_factory: IndividualFactory):
self.individual_factory = individual_factory
def mutate(self, individual: Individual):
mutated_genotype = list(individual.genotype)
mutation_probability = 1 / len(individual.genotype)
for index, gene in enumerate(individual.genotype):
if random.random() < mutation_probability:
mutated_genotype[index] = '0' if gene == '1' else '1'
return self.individual_factory.with_set_genotype(genotype = "".join(mutated_genotype))We encapsulate both concepts inside of the Breeder class. Its produce_offspring method takes the mating pool as a parameter.
class Breeder:
def __init__(self,
single_point_crossover: SinglePointCrossover,
mutator: Mutator):
self.single_point_crossover = single_point_crossover
self.mutator = mutator
def produce_offspring(self, parents):
offspring = []
number_of_parents = len(parents)
for index in range(int(number_of_parents / 2)):
parent_1, parent_2 = self.__pick_random_parents(parents, number_of_parents)
child_1, child_2 = self.single_point_crossover.crossover(parent_1, parent_2)
child_1_mutated = mutator.mutate(child_1)
child_2_mutated = mutator.mutate(child_2)
offspring.extend((child_1_mutated, child_2_mutated))
return offspring
def __pick_random_parents(self, parents, number_of_parents: int):
parent_1 = parents[random.randint(0, number_of_parents - 1)]
parent_2 = parents[random.randint(0, number_of_parents - 1)]
return parent_1, parent_2With each iteration the algorithm:
- Picks two individuals from the pool at random.
- Creates two new individuals by crossing over the genotypes of the selected parents.
- Mutates the genotypes of the newly created offspring.
- Adds so created individuals to the offspring collection, which will become the next generation.
putting all the pieces together
Now that we have all the conceptual components needed by a genetic algorithm ready, we can put them all together in the Environment class.
class Environment:
def __init__(self,
population_size: int,
parent_selector: ParentSelector,
population_factory: PopulationFactory,
breeder: Breeder):
self.population_factory = population_factory
self.population = self.population_factory.with_random_individuals(size = population_size)
self.parent_selector = parent_selector
self.breeder = breeder
def update(self):
parents = self.parent_selector.select_parents(self.population)
next_generation = breeder.produce_offspring(parents)
self.population = population_factory.with_individuals(next_generation)
def get_the_fittest(self, n: int):
return self.population.get_the_fittest(n)It takes care of initiating the population, and with each call to the update method, it does the parent selection, produces offspring, and replaces the current population with a new one. Additionally, it provides a way of getting the fittest individuals from the current population through the get_the_fittest method.
Finally, we need to instantiate all the parts, decide on some of the parameters (e.g. number of generations, genotype length, etc.), and iterate till we find a solution or run out of patience.
TOTAL_GENERATIONS = 10000
POPULATION_SIZE = 50
GENOTYPE_LENGTH = 20
current_generation = 1
genotype_decoder = GenotypeDecoder()
fitness_evaluator = FitnessEvaluator(genotype_decoder)
individual_factory = IndividualFactory(GENOTYPE_LENGTH, fitness_evaluator)
population_factory = PopulationFactory(individual_factory)
single_point_crossover = SinglePointCrossover(individual_factory)
mutator = Mutator(individual_factory)
breeder = Breeder(single_point_crossover, mutator)
parent_selector = ParentSelector()
environment = Environment(POPULATION_SIZE,
parent_selector,
population_factory,
breeder)
highest_fitness_list = []
while current_generation <= TOTAL_GENERATIONS:
fittest = environment.get_the_fittest(1)[0]
highest_fitness_list.append(fittest.fitness)
if "0" not in fittest.genotype:
print("Winner, winner, chicken dinner! We got there")
break
environment.update()
current_generation += 1
print("Stopped at generation " + str(current_generation - 1) + ". The fittest individual: ")
print(fittest)
import matplotlib.pyplot as plt
generations = range(1, len(highest_fitness_list) + 1)
plt.plot(generations, highest_fitness_list)
plt.title('Fittest individual in each generation')
plt.xlabel('Generation')
plt.ylabel('Fitness')
plt.show()We are going to opt for a modest 10000 generations, with a population of 50 individuals (if you modify this number, keep in mind it needs to be even). Finally, we print the fittest individual’s genotype and the generation number at which it was created after the algorithm has finished, and plot the fittest individual’s fitness in each generation.
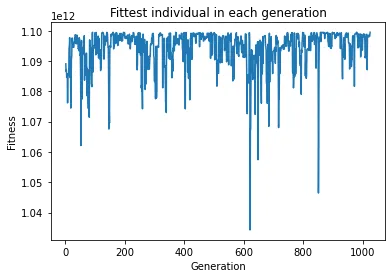
results
If you were brave enough to run the code, and you did it more than once, you will notice that the generation in which the solution is found varies between the runs significantly. This can be explained by a fair share of randomness inherent to the algorithm.
You might want to tune the parameters of the algorithm, such as the population size and the mutation probability (e.g. increasing the population size will most likely result in finding the solution quicker). Additionally, you might want to start with a population of minimal fitness, instead of a random population, and see how this changes the number of iterations needed over several runs (replace theself.population = self.population_factory.with_random_individuals(size = population_size) line with self.population = self.population_factory.with_minimal_fitness_individuals(size = population_size) inside of the Environment class).
Hopefully, the article and the code make some of the core concepts of Genetic Algorithms easier to comprehend. The implementation, being far from perfect, should be modular enough and easy to modify by switching up parts of the algorithm as needed (e.g. how an individual is represented, the fitness function, one-point crossover with n-point crossover, etc.). You can find the full code, as a jupyter notebook, here.
References:
[1] A.E. Eiben, J.E. Smith. Introduction to Evolutionary Computing.
[2] S. Luke. Essentials of Metaheuristics.
You can find the full source code on GitHub
Leave a Reply